---
title: 'Low-dimensional embeddings 1'
author: "Levi Waldron"
output: slidy_presentation
---
```{r setup, include=FALSE}
knitr::opts_chunk$set(eval = TRUE, cache=FALSE)
```
## Outline
Based on [Biomedical Data Science](https://genomicsclass.github.io/book/) by Irizarry and Love, chapter 8.
- Distances in high dimensions
- Principal Components Analysis and Singular Value Decomposition
- Multidimensional Scaling (Principal Coordinates Analysis)
- GenomicSuperSignatures Bioconductor package
Built slides at https://rpubs.com/lwaldron/916521
## Metrics and distances
A **metric** satisfies the following five properties:
1. non-negativity $d(a, b) \ge 0$
2. symmetry $d(a, b) = d(b, a)$
3. identification mark $d(a, a) = 0$
4. definiteness $d(a, b) = 0$ if and only if $a=b$
5. triangle inequality $d(a, b) + d(b, c) \ge d(a, c)$
- A **similarity function** satisfies 1-2, and **increases** as $a$ and $b$ become more similar
- A **dissimilarity function** satisfies 1-2, and **decreases** as $a$ and $b$ become more similar
## Euclidian distance (metric)
- Remember grade school:
```{r, echo=FALSE, fig.height=3.5}
rafalib::mypar()
plot(
c(0, 1, 1),
c(0, 0, 1),
pch = 16,
cex = 2,
xaxt = "n",
yaxt = "n",
xlab = "",
ylab = "",
bty = "n",
xlim = c(-0.25, 1.25),
ylim = c(-0.25, 1.25)
)
lines(c(0, 1, 1, 0), c(0, 0, 1, 0))
text(0, .2, expression(paste('(A'[x] * ',A'[y] * ')')), cex = 1.5)
text(1, 1.2, expression(paste('(B'[x] * ',B'[y] * ')')), cex = 1.5)
text(-0.1, 0, "A", cex = 2)
text(1.1, 1, "B", cex = 2)
```
Euclidean d = $\sqrt{ (A_x-B_x)^2 + (A_y-B_y)^2}$.
- **Side note**: also referred to as $L_2$ norm
## Euclidian distance in high dimensions
```{r, echo = FALSE, message=FALSE, warning=FALSE}
if(!require(tissuesGeneExpression)){
BiocManager::install("genomicsclass/tissuesGeneExpression")
}
if(!require(GSE5859)){
BiocManager::install("genomicsclass/GSE5859")
}
```
```{r}
## BiocManager::install("genomicsclass/tissuesGeneExpression") #if needed
## BiocManager::install("genomicsclass/GSE5859") #if needed
library(GSE5859)
library(tissuesGeneExpression)
data(tissuesGeneExpression)
dim(e) ##gene expression data
table(tissue) ##tissue[i] corresponds to e[,i]
```
Interested in identifying similar *samples* and similar *genes*
## Notes about Euclidian distance in high dimensions
- Points are no longer on the Cartesian plane
- instead they are in higher dimensions. For example:
- sample $i$ is defined by a point in 22,215 dimensional space: $(Y_{1,i},\dots,Y_{22215,i})^\top$.
- feature $g$ is defined by a point in 189 dimensions $(Y_{g,189},\dots,Y_{g,189})^\top$
Euclidean distance as for two dimensions. E.g., the distance between two samples $i$ and $j$ is:
$$ \mbox{dist}(i,j) = \sqrt{ \sum_{g=1}^{22215} (Y_{g,i}-Y_{g,j })^2 } $$
and the distance between two features $h$ and $g$ is:
$$ \mbox{dist}(h,g) = \sqrt{ \sum_{i=1}^{189} (Y_{h,i}-Y_{g,i})^2 } $$
## Euclidian distance in matrix algebra notation
The Euclidian distance between samples $i$ and $j$ can be written as:
$$ \mbox{dist}(i,j) = \sqrt{ (\mathbf{Y}_i - \mathbf{Y}_j)^\top(\mathbf{Y}_i - \mathbf{Y}_j) }$$
with $\mathbf{Y}_i$ and $\mathbf{Y}_j$ columns $i$ and $j$.
```{r}
t(matrix(1:3, ncol = 1))
matrix(1:3, ncol = 1)
t(matrix(1:3, ncol = 1)) %*% matrix(1:3, ncol = 1)
```
## Note about matrix algebra in R
- R is very efficient at "vectorized" matrix algebra
- for very large matricies, see the:
- [Matrix](https://CRAN.R-project.org/package=Matrix) CRAN package (sparse matrices)
- [rhdf5](https://bioconductor.org/packages/rhdf5/) and [DelayedArray](https://bioconductor.org/packages/DelayedArray/) Bioconductor package (on-disk arrays)
## 2-sample example
```{r}
kidney1 <- e[, 1]
kidney2 <- e[, 2]
colon1 <- e[, 87]
sqrt(sum((kidney1 - kidney2) ^ 2))
sqrt(sum((kidney1 - colon1) ^ 2))
```
## 3-sample example using dist()
```{r}
dim(e)
(d <- dist(t(e[, c(1, 2, 87)])))
class(d)
```
## The dist() function
Excerpt from ?dist:
```{r, eval=FALSE}
dist(x,
method = "euclidean",
diag = FALSE,
upper = FALSE,
p = 2)
```
- **method:** the distance measure to be used.
- This must be one of "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowski".
- `dist` class output from `dist()` is used for many clustering algorithms and heatmap functions
*Caution*: `dist(e)` creates a `r nrow(e)` x `r nrow(e)` matrix that will probably crash your R session.
## Note on standardization
- In practice, features (measures) should usually be "standardized" when calculating distances, for example by converting to z-score:
$$x_{gi} \leftarrow \frac{(x_{gi} - \bar{x}_g)}{s_g}$$
- This is done because the differences in overall amplitude between features may be technical, *e.g.*:
- GC bias, PCR amplification efficiency, ...
- Euclidian distance and $1-r$ (Pearson cor) are related:
- $\frac{d_E(x, y)^2}{2m} = 1 - r_{xy}$
- $m$ = \# dimensions
## Dimension reduction and PCA
- Motivation for dimension reduction
Simulate the heights of twin pairs:
```{r}
set.seed(1)
n <- 100
y <- t(MASS::mvrnorm(n, c(0, 0), matrix(c(1, 0.95, 0.95, 1), 2, 2)))
dim(y)
cor(t(y))
```
## Visualizing twin pairs data
```{r, echo=FALSE}
z1 = (y[1,] + y[2,]) / 2 #the sum
z2 = (y[1,] - y[2,]) #the difference
z = rbind(z1, z2) #matrix now same dimensions as y
thelim <- c(-3, 3)
rafalib::mypar(1, 2)
plot(
y[1,],
y[2,],
xlab = "Twin 1 (standardized height)",
ylab = "Twin 2 (standardized height)",
xlim = thelim,
ylim = thelim,
main = "Original twin heights"
)
points(y[1, 1:2], y[2, 1:2], col = 2, pch = 16)
plot(
z[1,],
z[2,],
xlim = thelim,
ylim = thelim,
xlab = "Average height",
ylab = "Difference in height",
main = "Manual PCA-like projection"
)
points(z[1, 1:2] , z[2, 1:2], col = 2, pch = 16)
```
## Not much distance is lost in the second dimension
```{r, echo=FALSE}
rafalib::mypar()
d = dist(t(y))
d3 = dist(z[1, ]) * sqrt(2) ##distance computed using just first dimension mypar(1,1)
plot(as.numeric(d),
as.numeric(d3),
xlab = "Pairwise distances in 2 dimensions",
ylab = "Pairwise distances in 1 dimension")
abline(0, 1, col = "red")
```
- Not much loss of height differences when just using average heights of twin pairs.
- because twin heights are highly correlated
## Singular Value Decomposition (SVD)
SVD generalizes the example rotation we looked at:
$$\mathbf{Y} = \mathbf{UDV}^\top$$
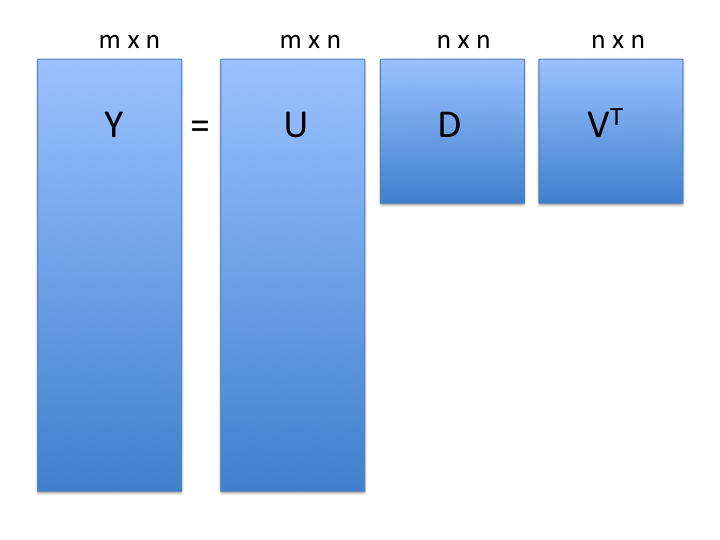 - **note**: the above formulation is for $m$ rows $> n$ columns
- $\mathbf{Y}$: the $m$ rows x $n$ cols matrix of measurements
- $\mathbf{U}$: $m \times n$ matrix relating original scores to PCA scores (**loadings**)
- $\mathbf{D}$: $n \times n$ diagonal matrix (**eigenvalues**)
- $\mathbf{V}$: $n \times n$ *orthogonal* matrix (**eigenvectors or PCA scores**)
- orthogonal = unit length and "perpendicular" in 3-D
## SVD of gene expression dataset
Scaling:
```{r}
e.standardized <- t(scale(t(e), center = TRUE, scale = FALSE))
```
SVD:
```{r}
s <- svd(e.standardized)
names(s)
```
## Components of SVD results
```{r}
dim(s$u) # loadings
length(s$d) # eigenvalues
dim(s$v) # d %*% vT = scores
```
- **note**: the above formulation is for $m$ rows $> n$ columns
- $\mathbf{Y}$: the $m$ rows x $n$ cols matrix of measurements
- $\mathbf{U}$: $m \times n$ matrix relating original scores to PCA scores (**loadings**)
- $\mathbf{D}$: $n \times n$ diagonal matrix (**eigenvalues**)
- $\mathbf{V}$: $n \times n$ *orthogonal* matrix (**eigenvectors or PCA scores**)
- orthogonal = unit length and "perpendicular" in 3-D
## SVD of gene expression dataset
Scaling:
```{r}
e.standardized <- t(scale(t(e), center = TRUE, scale = FALSE))
```
SVD:
```{r}
s <- svd(e.standardized)
names(s)
```
## Components of SVD results
```{r}
dim(s$u) # loadings
length(s$d) # eigenvalues
dim(s$v) # d %*% vT = scores
```
 ## PCA is a SVD
- gene expression dataset
```{r, cache=TRUE}
rafalib::mypar()
p <- prcomp(t(e.standardized))
plot(s$u[, 1] ~ p$rotation[, 1])
```
**Lesson:** u and v can each be multiplied by -1 arbitrarily
## PCA interpretation: loadings
## PCA is a SVD
- gene expression dataset
```{r, cache=TRUE}
rafalib::mypar()
p <- prcomp(t(e.standardized))
plot(s$u[, 1] ~ p$rotation[, 1])
```
**Lesson:** u and v can each be multiplied by -1 arbitrarily
## PCA interpretation: loadings
 - $\mathbf{U}$ (**loadings**): relate the *principal component* axes to the original variables
- think of principal component axes as a weighted combination of original axes
## Visualizing PCA loadings
```{r}
plot(p$rotation[, 1],
xlab = "Index of genes",
ylab = "Loadings of PC1",
main = "PC1 loadings of each gene")
abline(h = c(-0.03, 0.03), col = "red")
```
## Genes with high PC1 loadings
```{r, fig.height=3.5}
e.pc1genes <-
e.standardized[p$rotation[, 1] < -0.03 |
p$rotation[, 1] > 0.03,]
dim(e.pc1genes)
```
```{r, echo = FALSE}
pheatmap::pheatmap(
e.pc1genes,
scale = "none",
show_rownames = TRUE,
show_colnames = FALSE
)
```
## PCA interpretation: eigenvalues
- $\mathbf{D}$ (**eigenvalues**): standard deviation scaling factor that each decomposed variable is multiplied by.
```{r, fig.height=3, fig.width=5, echo=TRUE, fig.align='center'}
rafalib::mypar()
plot(
p$sdev ^ 2 / sum(p$sdev ^ 2) * 100,
xlim = c(0, 150),
type = "b",
ylab = "% variance explained",
main = "Screeplot"
)
```
## PCA interpretation: eigenvalues
Alternatively as cumulative % variance explained (using `cumsum()` function)
```{r, fig.height=4, echo=TRUE, fig.align='center'}
rafalib::mypar()
plot(
cumsum(p$sdev ^ 2) / sum(p$sdev ^ 2) * 100,
ylab = "cumulative % variance explained",
ylim = c(0, 100),
type = "b",
main = "Cumulative screeplot"
)
```
## PCA interpretation: scores
- $\mathbf{U}$ (**loadings**): relate the *principal component* axes to the original variables
- think of principal component axes as a weighted combination of original axes
## Visualizing PCA loadings
```{r}
plot(p$rotation[, 1],
xlab = "Index of genes",
ylab = "Loadings of PC1",
main = "PC1 loadings of each gene")
abline(h = c(-0.03, 0.03), col = "red")
```
## Genes with high PC1 loadings
```{r, fig.height=3.5}
e.pc1genes <-
e.standardized[p$rotation[, 1] < -0.03 |
p$rotation[, 1] > 0.03,]
dim(e.pc1genes)
```
```{r, echo = FALSE}
pheatmap::pheatmap(
e.pc1genes,
scale = "none",
show_rownames = TRUE,
show_colnames = FALSE
)
```
## PCA interpretation: eigenvalues
- $\mathbf{D}$ (**eigenvalues**): standard deviation scaling factor that each decomposed variable is multiplied by.
```{r, fig.height=3, fig.width=5, echo=TRUE, fig.align='center'}
rafalib::mypar()
plot(
p$sdev ^ 2 / sum(p$sdev ^ 2) * 100,
xlim = c(0, 150),
type = "b",
ylab = "% variance explained",
main = "Screeplot"
)
```
## PCA interpretation: eigenvalues
Alternatively as cumulative % variance explained (using `cumsum()` function)
```{r, fig.height=4, echo=TRUE, fig.align='center'}
rafalib::mypar()
plot(
cumsum(p$sdev ^ 2) / sum(p$sdev ^ 2) * 100,
ylab = "cumulative % variance explained",
ylim = c(0, 100),
type = "b",
main = "Cumulative screeplot"
)
```
## PCA interpretation: scores
 - $\mathbf{V}$ (**scores**): The "datapoints" in the reduced prinipal component space
- In some implementations (like `prcomp()`), scores are already scaled by eigenvalues: $\mathbf{D V^T}$
## PCA interpretation: scores
```{r, fig.height=5, echo=FALSE}
rafalib::mypar()
plot(
p$x[, 1:2],
xlab = "PC1",
ylab = "PC2",
main = "plot of p$x[, 1:2]",
col = factor(tissue),
pch = as.integer(factor(tissue))
)
legend(
"topright",
legend = levels(factor(tissue)),
col = 1:length(unique(tissue)),
pch = 1:length(unique(tissue)),
bty = 'n'
)
```
## Multi-dimensional Scaling (MDS)
- also referred to as Principal Coordinates Analysis (PCoA)
- a reduced SVD, performed on a distance matrix
- identify two (or more) eigenvalues/vectors that preserve distances
```{r}
d <- as.dist(1 - cor(e.standardized))
mds <- cmdscale(d)
```
```{r, echo=FALSE}
rafalib::mypar()
plot(mds, col = factor(tissue), pch = as.integer(factor(tissue)))
legend(
"topright",
legend = levels(factor(tissue)),
col = 1:length(unique(tissue)),
bty = 'n',
pch = 1:length(unique(tissue))
)
```
## Summary: distances and dimension reduction
- Signs of loadings and scores can be arbitrarily flipped
- Dimension reduction is only helpful if you have *correlated variables*
- Sensitive to skew and outliers, most useful for Gaussian (normal) data, although there are extensions
- PCA projection:
- is the most interpretable form of dimension reduction
- can be applied to new datasets using the inverse of the loadings matrix
- screeplot will show signs of over-fitting, can be tested by cross-validation
- MDS (PCoA) projection gives flexibility in distance/dissimilarity measure, but less interpretable
## GenomicSuperSignature example
+--------------------------+------------------------------------+
| Google Slides: | {width="64"} |
| | |
| | |
+--------------------------+------------------------------------+
```{r, echo=FALSE}
knitr::include_url("https://docs.google.com/presentation/d/e/2PACX-1vTIv_-UQXxNJaSpeh2RML69GdjwjO7FMED2uZZfJCo0xmi8ATNJlf_lvPUnr-baM4NmQBP_FMjArDXM/embed?start=false&loop=false&delayms=60000")
```
- $\mathbf{V}$ (**scores**): The "datapoints" in the reduced prinipal component space
- In some implementations (like `prcomp()`), scores are already scaled by eigenvalues: $\mathbf{D V^T}$
## PCA interpretation: scores
```{r, fig.height=5, echo=FALSE}
rafalib::mypar()
plot(
p$x[, 1:2],
xlab = "PC1",
ylab = "PC2",
main = "plot of p$x[, 1:2]",
col = factor(tissue),
pch = as.integer(factor(tissue))
)
legend(
"topright",
legend = levels(factor(tissue)),
col = 1:length(unique(tissue)),
pch = 1:length(unique(tissue)),
bty = 'n'
)
```
## Multi-dimensional Scaling (MDS)
- also referred to as Principal Coordinates Analysis (PCoA)
- a reduced SVD, performed on a distance matrix
- identify two (or more) eigenvalues/vectors that preserve distances
```{r}
d <- as.dist(1 - cor(e.standardized))
mds <- cmdscale(d)
```
```{r, echo=FALSE}
rafalib::mypar()
plot(mds, col = factor(tissue), pch = as.integer(factor(tissue)))
legend(
"topright",
legend = levels(factor(tissue)),
col = 1:length(unique(tissue)),
bty = 'n',
pch = 1:length(unique(tissue))
)
```
## Summary: distances and dimension reduction
- Signs of loadings and scores can be arbitrarily flipped
- Dimension reduction is only helpful if you have *correlated variables*
- Sensitive to skew and outliers, most useful for Gaussian (normal) data, although there are extensions
- PCA projection:
- is the most interpretable form of dimension reduction
- can be applied to new datasets using the inverse of the loadings matrix
- screeplot will show signs of over-fitting, can be tested by cross-validation
- MDS (PCoA) projection gives flexibility in distance/dissimilarity measure, but less interpretable
## GenomicSuperSignature example
+--------------------------+------------------------------------+
| Google Slides: | {width="64"} |
| | |
| | |
+--------------------------+------------------------------------+
```{r, echo=FALSE}
knitr::include_url("https://docs.google.com/presentation/d/e/2PACX-1vTIv_-UQXxNJaSpeh2RML69GdjwjO7FMED2uZZfJCo0xmi8ATNJlf_lvPUnr-baM4NmQBP_FMjArDXM/embed?start=false&loop=false&delayms=60000")
```




